Res Dev Med Educ. 13:16.
doi: 10.34172/rdme.33206
Original Article
Development and validation of the mathematics self-efficacy scale for university students
Nimtaj Sayah Sayari Data curation, Investigation, Writing – original draft, 1 
Mohammad Mahdi Shariat Bagheri Conceptualization, Project administration, Supervision, Writing – review & editing, 2, * 
Farah Lotfi Kashani Methodology, Resources, Software, 3 
Author information:
1Department of Psychology, Central Tehran Branch, Islamic Azad University, Tehran, Iran
2Department of Clinical Educational Psychology, Central Tehran Branch, Islamic Azad University, Tehran, Iran
3Department of Psychology, Tehran Medical Sciences Branch, Islamic Azad University, Tehran, Iran
Abstract
Background:
Academic underperformance in mathematics is widespread across all educational levels. To comprehend its causes, it is crucial to analyze various factors that impact academic advancement in mathematics through their interplay. The present study aimed to develop and validate a mathematics self-efficacy scale for university students.
Methods:
The research method was correlational and of instrument development type. The statistical population included all undergraduate students of Islamic Azad Universities in Tehran in 2021, of which 300 were selected as a sample using a multi-stage cluster random sampling method. In the process of scale construction, a set of items was initially selected based on a review of the research literature in the field of mathematics self-efficacy and the identification of valid tests in this area. Then, a preliminary version of the questionnaire was administered to a sample of 300 students. Factor analysis, Cronbach’s alpha coefficient, and Pearson correlation coefficient were used to analyze the data.
Results:
Based on the results of the exploratory factor analysis, the mathematics self-efficacy scale consisted of four components: mathematical achievement and success, general mathematical self-efficacy, mathematical anxiety, and mathematical stress. Cronbach’s alpha for the four components were 0.97, 0.95, 0.95, and 0.93, respectively. The results of the convergent validity evaluation showed that all four components of the mathematics self-efficacy scale were positively correlated with the intrinsic and extrinsic motivation components of the Academic Motivation Scale and negatively correlated with academic motivation.
Conclusion:
The components of the mathematics self-efficacy scale had acceptable internal consistency and convergent validity. Therefore, it can be concluded that the designed scale can be used as a valid tool to measure the level of mathematics self-efficacy in university students.
Keywords: Mathematics self-efficacy, Validity, Reliability, Exploratory factor analysis, University students
Copyright and License Information
© 2024 The Author(s).
This is an open access article distributed under the terms of the Creative Commons Attribution License (
http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, as long as the
original authors and source are cited. No permission is required from the authors or the publishers.
Funding Statement
There was no funding source.
Introduction
The topic of students’ academic achievement and the factors influencing it has been of interest to psychologists and educators since ancient times.1 Given the importance of mathematics in various fields and educational levels, one of the goals of the educational system is to include mathematical concepts in the curriculum.2 In addition to developing students’ cognitive abilities and reasoning skills, this prepares them for future scientific and technological advancements.3 Considering the high rate of academic failure in this subject, it is essential to provide appropriate instruction and consider factors that can improve the quality of mathematics education.4
The prevalence of academic failure in mathematics is a common problem for students at all levels of education. Students’ performance in mathematics is not satisfactory. Therefore, to identify the causes, it is necessary to investigate the complex interplay of both internal and external factors affecting academic achievement in mathematics.5 Difficulties in learning mathematics can either stem from the subject itself or external factors. Problems related to mathematics itself are rooted in its content, nature, and abstractness. External factors can be either intrapersonal or interpersonal in origin. Intrapersonal factors relate to individual characteristics of students in terms of cognitive processes, learning, motivation, and attitude. Interpersonal factors involve issues that are not related to mathematics or individual characteristics but are influenced by cultural, social, and educational factors, teaching methods, and teacher interactions.6
Self-efficacy is a key construct in Bandura’s social cognitive theory and is defined as an individual’s beliefs about their capabilities to organize and execute courses of action required to produce given attainments.7 It is a powerful predictor of academic achievement, including mathematics performance. Self-efficacy is a unique belief that influences motivation. It can help individuals determine their effort to undertake an activity, their persistence when facing challenges, and their resilience when facing unfavorable situations.8,9 Kaskens et al10 found that self-concept and self-efficacy were positive predictors of mathematics achievement, while mathematics anxiety had adversely affected students’ mathematical progress. Rozgonjuk et al11 reported that students’ success in mathematics is positively correlated with mathematics self-efficacy and negatively correlated with mathematics anxiety. Živković et al12 showed that mathematics self-efficacy was a significant predictor of successful completion of special mathematics tasks, and mathematics interest was a predictor of mathematics grades. Tossavainen et al13 found that higher motivation self-efficacy, and intrinsic and utility values toward mathematics, led to better performance in mathematics tasks.
Individuals’ performance in a specific task domain is highly dependent on their beliefs about their abilities in that domain. In the context of mathematics, mathematical self-efficacy can be defined as an individual’s situational assessment of their confidence in their ability to successfully perform or complete a specific mathematical task or problem.14 Sakellariou et al15 investigated the relationship between Bandura’s four sources of self-efficacy and mathematical self-efficacy. The findings revealed that students with high or low self-efficacy not only experience different levels of exposure to self-efficacy sources but also hold different perspectives on the impact of each source on their mathematical self-efficacy. Doménech-Betoret et al16 showed that students perceive their self-efficacy based on the growth of self-efficacy sources that have occurred in their lives, particularly the amount of mastery experiences they have completed.
Numerous studies have accentuated the crucial role of mathematical self-efficacy in explaining and predicting students’ mathematical and academic performance.17,18 This implies that students with higher mathematical self-efficacy are more likely to succeed in mathematics. Therefore, developing a valid instrument to measure mathematical self-efficacy in university students is of great importance. Various instruments have been developed by researchers to assess the concept of mathematical self-efficacy beliefs.19,20 However, these questionnaires are mostly designed for schoolchildren and their items do not apply to university students. Additionally, existing questionnaires for students do not comprehensively assess mathematical self-efficacy and fail to address all its dimensions. Considering the importance of mathematical self-efficacy in students’ academic and social lives and the need for a comprehensive assessment of this construct considering its various dimensions, it is necessary to measure this variable using reliable methods. Therefore, the present study was conducted to develop and validate a mathematical self-efficacy scale for university students.
Materials and Methods
Design and the study sample
The research method was correlational and of the instrument development type. The statistical population included all undergraduate students of Islamic Azad Universities in Tehran in 2021, of which 300 were selected as the sample using a multi-stage cluster random sampling method. In the first stage, a list of universities was prepared and four universities were randomly selected. Then, three faculties were randomly selected from each university. In the next stage, the research sample was selected from among the students who were willing to participate in the research. To develop the questionnaire, first, a review of the research literature in the field of mathematical self-efficacy was conducted to identify existing instruments. After identifying the existing instruments, a set of items was selected based on the sources of self-efficacy. In addition, some items were designed to assess the individual’s confidence in performing certain mathematical calculations or performing them, in addition to their self-efficacy beliefs. In this study, the confidence in the ability to perform mathematical calculations specific to the student context and at different levels of courses, as well as self-efficacy beliefs, were investigated. The instrument was reviewed by three psychology professors for readability and lack of ambiguity. The results of the reliability analysis showed that the initial form had a desirable level of initial reliability. After the final revision and clarification of ambiguities, the tests were administered.
Measures
Usher and Pajares’s Mathematics Self-Efficacy Scale
This scale is a 24-item questionnaire developed by Usher and Pajares20 to assess students’ perceptions of their self-efficacy in regulating their behavior when performing mathematical tasks. The items are based on Bandura’s theory of the four sources of self-efficacy. The scale has four subscales (mastery experiences, vicarious experiences, social persuasion, and physiological states), each with six items. The scale is answered using a 5-point Likert scale from 1 (never) to 5 (always). The initial internal consistency coefficient of the test was 0.838, with a mean of 78.53 and a standard deviation of 18.01. The minimum item-to-total correlation was 0.18 (item 21) and the maximum was 0.88 (item 18). Items 2, 19, 20, 21, 22, 23, and 24 had negative correlations. These items were re-evaluated along with the opinions of the professors regarding the content, readability, and appropriateness, and after applying the modifications, the tests were re-administered.
Mathematics Self-Confidence Test
This test consists of 8 items. The initial internal consistency coefficient of the test was obtained as 0.94, with a mean of 35.78 and a standard deviation of 9.36. The minimum item-to-total correlation was 0.70 (item 4) and the maximum was 0.84 (item 6). The items were re-evaluated along with the opinions of the professors regarding the content, readability, and appropriateness, and after applying the modifications, the tests were re-administered.
Mathematics Self-Efficacy and Anxiety Questionnaire
This questionnaire consists of 28 items and is in the form of a 5-point Likert scale. It was developed by May.21 13 items measure general self-efficacy and 15 items measure math anxiety and stress. The overall reliability of the scale was 0.96 using Cronbach’s alpha method. In terms of validity, there is a correlation between this scale and the Usher and Pajares’s20 scale. The initial internal consistency coefficient of the test was obtained as 0.626, with a mean of 86.25 and a standard deviation of 10.38. The minimum item-to-total correlation was 0.006 (item 10) and the maximum was 0.58 (item 8). Items 1, 4, 7, 23, 21, 19, 13, and 28 had negative correlations. These items were re-evaluated along with the opinions of the professors regarding the content, readability, and appropriateness, and after applying the modifications, the tests were re-administered.
The Academic Motivation Scale
The Academic Motivation Scale was developed by Vallerand et al.22 This scale is based on the Self-Determination Theory and consists of 28 items that measure three dimensions of motivation: intrinsic motivation, extrinsic motivation, and amotivation. The scale uses a 7-point Likert scale for scoring. Scores on the Academic Motivation Scale indicate low motivation (28-70), average motivation (70-112), or high motivation (above 112). The scale can be used to measure academic motivation in students of all ages and in a variety of settings.
Statistical analysis
The data collected were analyzed using the exploratory factor analysis method and the principal component analysis method. Cronbach’s alpha was used to assess the internal consistency of the items of the mathematical self-efficacy scale components. To assess convergent validity, the correlation coefficients of each of the four components with the dimensions of the academic motivation questionnaire were examined.
Results
The demographic findings revealed that 86 (28.67%) of the participants were younger than 22 years old, 160 (53.33%) were 23 to 25 years old, 15 (5.0%) were 26 to 28 years old, and 39 (13.0%) were older than 28 years old. The mean and standard deviation of the participants’ age were 23.66 and 5.33 years, respectively. 100 (33.33%) of the participants were male and 200 (66.67%) were female. Table 1 presents the means, standard deviations (SD), skewness, and kurtosis of each item in the mathematics self-efficacy and anxiety questionnaire, Usher and Pajares’s mathematics self-efficacy scale, and mathematics self-confidence test. As can be seen from Table 1, the skewness and kurtosis values of all items are within the ± 2 range. This finding indicates that the data distribution for each item is normal.
Table 1.
Means, SD, skewness, and kurtosis of each item of the research instruments
|
Items
|
Mean±SD
|
Skewness (kurtosis)
|
|
Tool name: Mathematics Self-efficacy and Anxiety Questionnaire
|
| 1 |
3.49 ± 1.19 |
-0.28 (-0.79) |
| 2 |
3.05 ± 1.31 |
-0.05 (-1.06) |
| 3 |
3.78 ± 1.32 |
-0.78 (-0.39) |
| 4 |
3.65 ± 1.12 |
-0.62 (-0.31) |
| 5 |
3.22 ± 1.39 |
-0.11 (-1.18) |
| 6 |
3.04 ± 1.30 |
-0.07 (-1.04) |
| 7 |
3.63 ± 1.13 |
-0.46 (-0.42) |
| 8 |
3.06 ± 1.25 |
0.11 (-0.79) |
| 9 |
3.34 ± 1.32 |
-0.29 (-0.98) |
| 10 |
3.09 ± 1.25 |
0.12 (-0.96) |
| 11 |
4.09 ± 1.06 |
-1.06 (0.49) |
| 12 |
3.89 ± 1.04 |
-0.82 (0.30) |
| 13 |
3.59 ± 1.16 |
-0.51 (-0.37) |
| 14 |
3.68 ± 1.37 |
-0.69 (-0.76) |
| 15 |
3.75 ± 1.32 |
-0.83 (-0.44) |
| 16 |
3.78 ± 1.09 |
-0.64 (-0.22) |
| 17 |
3.14 ± 1.23 |
-0.09 (-0.86) |
| 18 |
3.15 ± 1.29 |
-0.12 (-1.04) |
| 19 |
3.31 ± 1.18 |
-0.14 (-0.74) |
| 20 |
3.46 ± 1.23 |
-0.35 (-0.89) |
| 21 |
3.25 ± 1.28 |
-0.09 (-1.00) |
| 22 |
3.44 ± 1.32 |
-0.40 (-0.78) |
| 23 |
3.57 ± 1.05 |
-0.36 (-0.48) |
| 24 |
3.05 ± 1.18 |
0.10 (-0.81) |
| 25 |
3.37 ± 1.12 |
-0.35 (-0.41) |
| 26 |
3.19 ± 1.41 |
-0.27 (-1.22) |
| 27 |
3.01 ± 1.49 |
-0.12 (-1.39) |
| 28 |
3.15 ± 1.32 |
0.11 (-1.27) |
|
Tool name: Usher and Pajares's Mathematics Self-Efficacy Scale
|
| 1 |
3.30 ± 1.43 |
0.29 (-0.38) |
| 2 |
4.5 ± 1.29 |
-0.67 (-0.06) |
| 3 |
3.59 ± 1.40 |
0.12 (-0.62) |
| 4 |
3.10 ± 1.55 |
0.33 (-0.74) |
| 5 |
3.86 ± 1.63 |
-0.12 (-1.06) |
| 6 |
3.50 ± 1.68 |
0.14 (-0.74) |
| 7 |
3.86 ± 1.66 |
0.10 (-1.09) |
| 8 |
3.81 ± 1.68 |
-0.06 (-1.17) |
| 9 |
3.73 ± 1.59 |
-0.02 (-0.97) |
| 10 |
3.51 ± 1.78 |
0.08 (-1.29) |
| 11 |
3.39 ± 1.70 |
-0.16 (-1.07) |
| 12 |
3.64 ± 1.58 |
-0.08 (-0.96) |
| 13 |
3.64 ± 1.73 |
-0.29 (-0.15) |
| 14 |
3.43 ± 1.71 |
-1.10 (-1.14) |
| 15 |
3.29 ± 1.31 |
-0.69 (-0.58) |
| 16 |
3.33 ± 1.62 |
-1.01 (-0.14) |
| 17 |
3.26 ± 1.59 |
0.42 (-0.70) |
| 18 |
3.47 ± 1.72 |
-0.12 (-1.17) |
| 19 |
4.27 ± 1.65 |
-0.74 (-0.45) |
| 20 |
3.25 ± 1.76 |
0.37 (-1.10) |
| 21 |
4.64 ± 1.62 |
1.02 (-0.18) |
| 22 |
4.47 ± 1.62 |
-0.74 (-0.61) |
| 23 |
4.61 ± 1.52 |
-0.86 (-0.18) |
| 24 |
4.64 ± 1.68 |
-1.05 (-0.08) |
|
Toll name: Mathematics Self-Confidence Test
|
| 1 |
4.89 ± 1.24 |
-1.35 (1.07) |
| 2 |
4.28 ± 1.47 |
-0.66 (-0.38) |
| 3 |
4.30 ± 1.56 |
-0.74 (-0.51) |
| 4 |
4.78 ± 1.46 |
-1.24 (0.77) |
| 5 |
4.45 ± 1.56 |
-0.86 (-0.24) |
| 6 |
4.34 ± 1.36 |
-0.78 (-0.64) |
| 7 |
4.32 ± 1.33 |
-0.69 (-0.01) |
| 8 |
4.00 ± 1.41 |
-0.38 (-0.55) |
To determine the underlying factors of the mathematics self-efficacy scale based on the mathematics self-efficacy and anxiety questionnaire, Usher and Pajares’s mathematics self-efficacy scale, and mathematics self-confidence test, the collected data were analyzed using the exploratory factor analysis method and the principal component analysis method. The use of the principal component analysis method showed that the Kaiser-Meyer-Olkin (KMO) measure was 0.932. This index indicated that the sample size was adequate for exploratory factor analysis. The results also showed that Bartlett’s sphericity test was statistically significant; therefore, it can be concluded that the items were not independent of each other and there was an acceptable level of correlation between them.
Exploratory factor analysis revealed a seven-factor solution with eigenvalues exceeding one. These factors collectively explained approximately 75.0% of the total variance in the data (Table 2). The first factor emerged as the most dominant, accounting for 43.60% of the variance, while the seventh factor explained a smaller proportion (2.23%) (Table 2).
Table 2.
Number of components, eigenvalues, percentage of total variance, and cumulative variance
|
Components
|
Eigenvalues
|
% Of variance
|
Cumulative %
|
| 1 |
22.34 |
43.60 |
21.52 |
| 2 |
6.67 |
13.08 |
39.12 |
| 3 |
2.69 |
5.28 |
53.64 |
| 4 |
2.51 |
4.92 |
62.50 |
| 5 |
1.67 |
3.28 |
66.93 |
| 6 |
1.29 |
2.52 |
70.93 |
| 7 |
1.14 |
2.23 |
74.91 |
Further evaluation of the scree plot showed a break between the fourth and fifth factors, suggesting that the scree test indicated four factors, which have eigenvalues greater than 2 and explain about 66.88% of the variance (Figure 1).
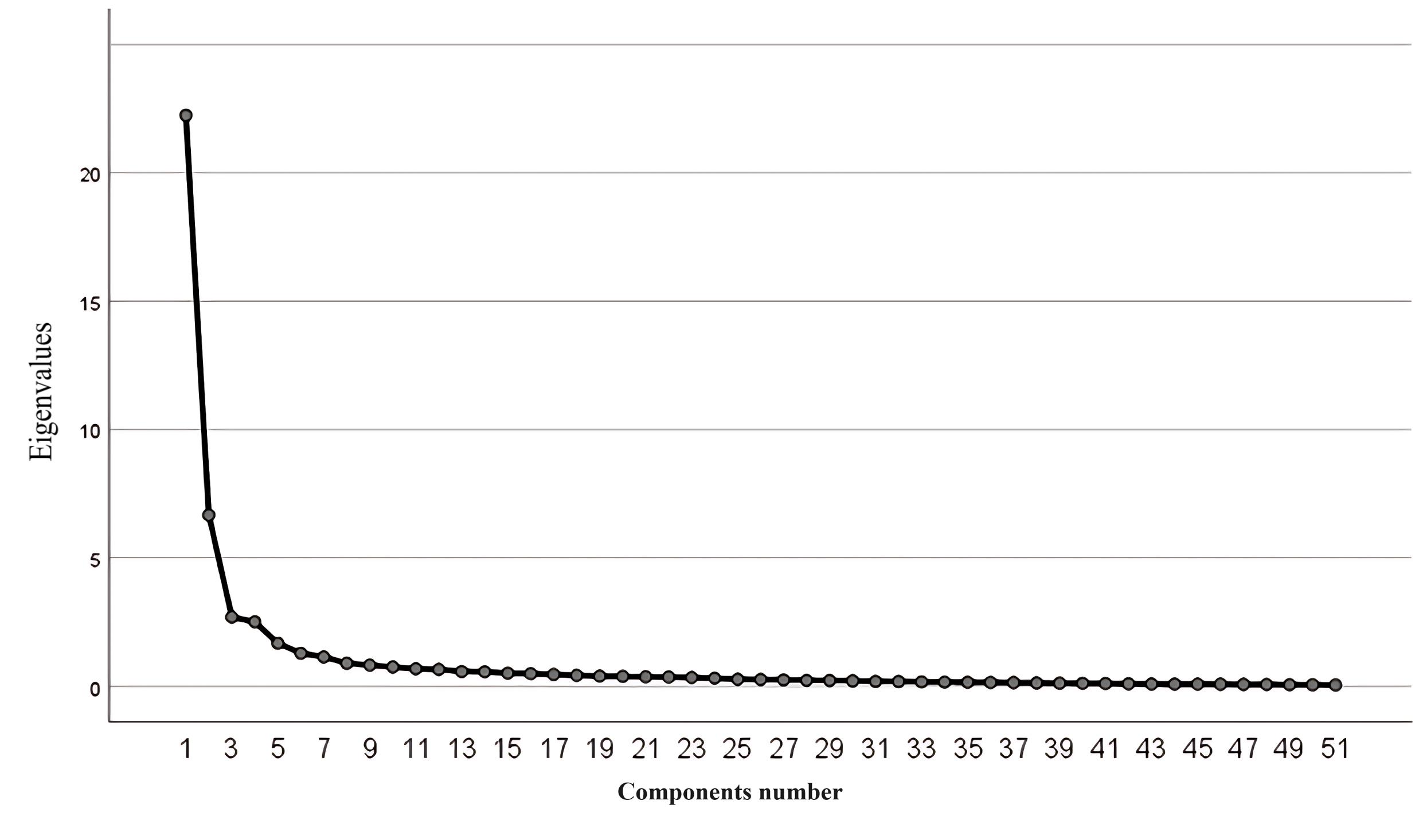
Figure 1.
Scree plot for determining component numbers
.
Scree plot for determining component numbers
To determine the number of components, Varimax rotation was employed to extract the factors. According to the results, items 12, 3, 15, 17, 18, 16, 14, 6, 13, 1, 4, 11, 9, 5, 8, 7, and 2 of the Usher and Pajares’s mathematics self-efficacy scale formed the first component; items 16, 20, 13, 19, 9, 23, 7, 12, 21, 4, 10, 1, 28, 3, and 14 of the mathematics self-efficacy and anxiety questionnaire formed the second component; items 18, 8, 6, 27, 25, 24, 17, 2, 26, 15, 22, 11, and 5 of the mathematics self-efficacy and anxiety questionnaire formed the third component; and items 21, 24, 19, 23, and 22 of the Usher and Pajares’s mathematics self-efficacy scale formed the fourth component of the new instrument.
Following the extraction of the factors, they were named based on the similarity of the items in each factor: Component 1 was named mathematical achievements and success, Component 2 was named general mathematical self-efficacy, Component 3 was named mathematical anxiety, and Component 4 was named mathematical stress. Therefore, it was concluded that the mathematics self-efficacy scale consists of four components: mathematical achievements and success, general mathematical self-efficacy, mathematical anxiety, and mathematical stress.
The internal consistency of the items of the mathematics self-efficacy scale was assessed using Cronbach’s alpha. According to the results of Table 3, Cronbach’s alpha coefficients of the components of mathematical achievements and success, general mathematical self-efficacy, mathematical anxiety, and mathematical stress were 0.97, 0.95, 0.95, and 0.93, respectively. This indicates the desirable internal consistency of the components of the mathematics self-efficacy scale. Therefore, it was concluded that the components of the mathematics self-efficacy scale have acceptable internal consistency.
Table 3.
Means, SD, Cronbach’s alpha coefficients, and correlation coefficients between the components of the mathematics self-efficacy scale and academic motivation scale
|
Variables
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
| 1- Mathematical achievements and success |
1 |
|
|
|
|
|
|
| 2- General mathematical self-efficacy |
0.48** |
1 |
|
|
|
|
|
| 3- Mathematical anxiety |
-0.52** |
-0.76** |
1 |
|
|
|
|
| 4- Mathematical stress |
-0.60** |
-0.37** |
0.42** |
1 |
|
|
|
| 5- Academic motivation- Intrinsic motivation |
0.21* |
0.27* |
0.17* |
0.15* |
1 |
|
|
| 6- Academic motivation- Extrinsic motivation |
0.22* |
0.29* |
0.23* |
0.07 |
0.60** |
1 |
|
| 7- Academic motivation- Amotivation |
-0.30** |
-0.36** |
-0.21* |
-0.19 |
-0.56** |
-0.63** |
1 |
| Mean ± SD |
65.09 ± 23.50 |
52.65 ± 14.06 |
42.51 ± 13.06 |
22.62 ± 7.21 |
54.98 ± 12.20 |
57.38 ± 13.2 |
13.98 ± 6.24 |
| Cronbach's alpha coefficients |
0.97 |
0.95 |
0.95 |
0.93 |
0.82 |
0.86 |
0.85 |
To evaluate the convergent validity of the mathematics self-efficacy scale, the correlation coefficients of each of its four factors with the dimensions of the academic motivation questionnaire were examined. As Table 3 shows, all four factors of the mathematics self-efficacy questionnaire were positively correlated with the intrinsic and extrinsic motivation factors of the academic motivation questionnaire and negatively correlated with academic disengagement. This finding indicates that the mathematics self-efficacy questionnaire has acceptable convergent validity.
Discussion
The present study aimed to construct and validate a mathematics self-efficacy scale for university students. Based on the results, the mathematics self-efficacy scale consisted of four components: mathematical achievements and success, general mathematical self-efficacy, mathematical anxiety, and mathematical stress. Regarding the mathematical achievements and success factor, the findings are in line with the research of Sukoco and Suharjo,23 which showed a close relationship between mathematical self-efficacy and students’ mathematical performance/achievement. Sakellariou et al15 also confirmed the relationship between the four sources of Bandura’s predictive self-efficacy and mathematical self-efficacy. In this regard, Bandura7 argues that people’s beliefs in their self-efficacy form a major part of their self-awareness. Four important sources have been identified for creating and changing self-efficacy beliefs: mastery experiences, vicarious experiences, verbal persuasion, and physiological states.
Individuals engage in activities and tasks, interpret the results of their actions, use these interpretations to develop their beliefs about their abilities to engage in subsequent tasks and activities and act in accordance with the beliefs they have created. Typically, when people interpret the behavioral outcomes of their actions as successful, it increases their self-efficacy; unfavorable behavioral outcomes decrease self-efficacy.24 However, individuals with low self-efficacy often underestimate their successes rather than changing their self-beliefs. Even after individuals achieve success through hard work, some of them doubt their ability to repeat such hard work. Consequently, mastery experiences are only raw data, and several factors influence how this information is cognitively processed and affect the individual’s self-assessments. People’s successes create strong beliefs in their effectiveness, and failures reduce it.20
Mastery experiences provide the performer with first-hand information about their effectiveness. Previous successes based on personal mastery provide immediate and tangible evidence of whether or not the person can succeed in a particular task. Personal mastery is cultivated by providing opportunities to complete challenging tasks, which ultimately lead to the achievement of desired goals. The method is to start with easy tasks and then proceed in small steps towards more difficult tasks until the person feels a sense of mastery over all the complexities of the problems.25 Bandura7 points out that successes strengthen efficacy beliefs, and failures, especially if they occur before a sense of efficacy is developed, weaken self-efficacy beliefs. Performances that do not lead to the desired results lead to lower efficacy. A sense of self-efficacy is created when the individual can overcome obstacles with perseverance and continuous effort. When people believe that they have what it takes to succeed, they are more persistent in the face of adversity and become stronger and more capable of enduring hardships. Experiences that provide confidence in one’s abilities allow one to tolerate problems and failures without losing one’s worth. The amount of impact that the performance of each behavior has on self-efficacy depends on the strength of the individual’s expectations. If an individual’s behavioral history has created a strong sense of efficacy, occasional inadequate performance will not change self-efficacy significantly.26 However, when the performer is inexperienced and the sense of efficacy is not yet firmly established, failures and successes will have a significant impact on the future sense of efficacy. Of the sources of efficacy expectations, personal behavioral history is the most important.27
Regarding the general mathematical self-efficacy component, researchers have found that differences in success in mathematics can be partially explained by individuals’ self-beliefs about their mathematical abilities.28 One of the key self-beliefs is self-efficacy, which includes students’ mathematical self-efficacy. Mathematical self-efficacy is the confidence that a student has in their ability to solve mathematical problems, complete mathematical tasks, and succeed in mathematics-related academic fields.29
According to Bandura’s theory, the role of self-efficacy beliefs in human functioning is that individuals’ motivation, emotional states, and actions are more based on what they believe than on what the case is.7 Therefore, how individuals behave is better predicted by their beliefs about their abilities than by what they do. In this way, self-efficacy perceptions help individuals determine what to do with the knowledge and skills they have. This helps us to explain why individuals’ behaviors sometimes differ from their actual abilities and why their behaviors vary widely even when they have the same knowledge. For example, some highly talented individuals suffer from doubts about their abilities and capabilities that they clearly possess and feel helpless, while others (with relatively few skills) are confident in what they can do, even though their skill set is relatively small. Belief and reality rarely coincide, and individuals are typically guided by their beliefs. As a result, in general, individuals’ progress and achievements can be better predicted by their self-efficacy beliefs than by their knowledge, skills, and previous achievements.
Regarding the extraction of the two components of mathematical anxiety and stress as components of mathematical self-efficacy, the findings are consistent with the research of Zakariya,14 who found that students’ mathematical self-efficacy beliefs are affected by emotional-physiological arousal, and with the research of Hiller et al,30 who showed that there is a relationship between mathematical anxiety and self-efficacy. Students who enjoy mathematics and engaging in activities that require the application of mathematical knowledge are more likely to achieve academic success in mathematics. Conversely, students who experience a range of negative emotions, from restlessness and unease to confusion, distress, and panic, towards mathematics will be less successful in this subject.31
In terms of explaining the two components of mathematical stress and anxiety, it can be said that emotional and physical states, such as anxiety, stress, arousal, and mood states, provide information about efficacy beliefs. Individuals can measure their confidence by experiencing their emotional states when thinking about an activity. The occurrence of strong emotional reactions to a task provides the individual with cues to predict the outcome of success or failure in that task. When individuals experience negative thoughts and fear about their abilities, these negative reactions can lower self-efficacy perceptions, leading to increased stress and anxiety, and ultimately making the individual feel incompetent about the performance they fear. One way to increase self-efficacy beliefs is to improve emotional and physical health and reduce negative emotional states. Because individuals can change their thoughts and feelings, increasing self-efficacy beliefs can have a strong impact on physiological states.
Individuals interpret their stress and tension reactions as signs of vulnerability to poor performance. In stressful situations, individuals perceive their physiological activities as indicators of imbalance or disruption. Negative emotions can cause tension and pressure, disrupting individuals from within and ultimately having a negative impact on their efficacy. Individuals’ perceptions of their physiological states, such as fear, anxiety, tension, and depression, can lead them to underestimate their abilities to perform tasks and lower their personal self-efficacy expectations.32 Indices of physiological efficacy are not limited to automatic or involuntary emotions, but also encompass other physiological indices, such as individuals’ tolerance and endurance of the aforementioned indicators, which are considered factors of physical inefficiency. However, it is not only the intensity of emotional and physical reactions that matters, but also how they are perceived and interpreted. Individuals with high self-efficacy are more likely to interpret their arousal as energizing and facilitating performance, while those who are highly doubtful of their abilities see their arousal as a disabling factor. The causal relationship between efficiency and physiological arousal is bidirectional. Inefficiency increases arousal, and increased arousal reinforces the perception of inefficiency.33
The results showed that all four components of the mathematics self-efficacy scale were positively correlated with the intrinsic and extrinsic motivation components of the academic motivation scale and negatively correlated with academic amotivation. This finding indicates that the mathematics self-efficacy questionnaire had acceptable convergent validity. In this regard, the results of various studies have shown the relationship between self-efficacy and academic motivation.34,35 This means that students’ academic activities are influenced by their self-efficacy beliefs. Students with high self-efficacy have higher academic motivation and achievement, and are more likely to overcome academic challenges.
Motivation is a very important factor for success, especially in academic fields such as mathematics.36 Motivation can be defined as the activating, energizing, sustaining, and directing of behavior towards a goal. It is believed that motivational behaviors are closely related to the beliefs that students have about themselves and their tasks. These beliefs include the criteria that individuals use to choose how to approach a task. These personal criteria, regardless of the conditions and how they are presented, play a fundamental role in personal motivation.37 In fact, students’ motivational beliefs are considered to be determinants of self-efficacy. Therefore, the relationship between motivational components (intrinsic goal orientation, extrinsic goal orientation, task value, and learning performance self-efficacy) and mathematical self-efficacy can be explained as follows: motivation, as the primary cause and driver of behavior, strengthens students’ academic behaviors and also directs their academic behaviors towards activities and programs that lead to academic achievement.
Study limitations
The study only involved undergraduate students from Islamic Azad Universities in Tehran in 2021. This limits the generalizability of the findings to other university populations, educational systems, or years. The experiences and factors impacting mathematics self-efficacy might differ across student demographics, cultures, and educational contexts. The study relies on self-reported data from students for both the newly developed mathematics self-efficacy scale and the academic motivation scale.
Conclusion
In conclusion, the present study has developed and validated a reliable and valid mathematics self-efficacy scale for university students. The scale’s multidimensional structure, encompassing both positive (achievement, general self-efficacy) and negative (anxiety, stress) aspects, allows for a nuanced understanding of self-efficacy in the context of mathematics learning. This instrument holds promise for future research investigating the complex interplay between self-efficacy, motivation, and academic achievement in mathematics education.
Acknowledgments
We extend our appreciation to all students who generously volunteered to contribute to this research study.
Competing Interests
The authors declared no conflicts of interest.
Ethical Approval
Not applicable.
References
- Arian M, Kamali A, Oghazian MB. Comparing the efficacy of problem-based learning vs lectures on the academic achievement and educational motivation of nursing students: a 3-year quasi-experimental study. Res Dev Med Educ 2022; 11(1):3. doi: 10.34172/rdme.2022.003 [Crossref] [ Google Scholar]
- Gravemeijer K, Stephan M, Julie C, Lin FL, Ohtani M. What mathematics education may prepare students for the society of the future?. Int J Sci Math Educ 2017; 15(1):105-23. doi: 10.1007/s10763-017-9814-6 [Crossref] [ Google Scholar]
- Edelsbrunner PA, Schumacher R, Stern E. Children’s scientific reasoning in light of general cognitive development. In: Houdé O, Borst G, editors. The Cambridge Handbook of Cognitive Development. Cambridge: Cambridge University Press; 2022. p. 585-605.
- Fathiazar E, Mani A, Adib Y, Sharifi Z. Effectiveness of an educational neuroscience-based curriculum to improve academic achievement of elementary students with mathematics learning disabilities. Res Dev Med Educ 2020; 9(1):18. doi: 10.34172/rdme.2020.018 [Crossref] [ Google Scholar]
- Hossein-Mohand H, Hossein-Mohand H. Influence of motivation on the perception of mathematics by secondary school students. Front Psychol 2022; 13:1111600. doi: 10.3389/fpsyg.2022.1111600 [Crossref] [ Google Scholar]
- Brezavšček A, Jerebic J, Rus G, Žnidaršič A. Factors influencing mathematics achievement of university students of social sciences. Mathematics 2020; 8(12):2134. doi: 10.3390/math8122134 [Crossref] [ Google Scholar]
- Bandura A. Self-efficacy: toward a unifying theory of behavioral change. Psychol Rev 1977; 84(2):191-215. doi: 10.1037//0033-295x.84.2.191 [Crossref] [ Google Scholar]
- Su A, Wan S, He W, Dong L. Effect of intelligence mindsets on math achievement for Chinese primary school students: math self-efficacy and failure beliefs as mediators. Front Psychol 2021; 12:640349. doi: 10.3389/fpsyg.2021.640349 [Crossref] [ Google Scholar]
- Hosseinabadi P, Asgari P, Bakhtiarpour S. Predicting research self-efficacy through spiritual intelligence and academic stress in medical students. Res Dev Med Educ 2023; 12(1):21. doi: 10.34172/rdme.2023.33132 [Crossref] [ Google Scholar]
- Kaskens J, Segers E, Goei SL, van Luit JEH, Verhoeven L. Impact of Children’s math self-concept, math self-efficacy, math anxiety, and teacher competencies on math development. Teach Teach Educ 2020; 94:103096. doi: 10.1016/j.tate.2020.103096 [Crossref] [ Google Scholar]
- Rozgonjuk D, Kraav T, Mikkor K, Orav-Puurand K, Täht K. Mathematics anxiety among STEM and social sciences students: the roles of mathematics self-efficacy, and deep and surface approach to learning. Int J STEM Educ 2020; 7(1):46. doi: 10.1186/s40594-020-00246-z [Crossref] [ Google Scholar]
- Živković M, Pellizzoni S, Doz E, Cuder A, Mammarella I, Passolunghi MC. Math self-efficacy or anxiety? The role of emotional and motivational contribution in math performance. Soc Psychol Educ 2023; 26(3):579-601. doi: 10.1007/s11218-023-09760-8 [Crossref] [ Google Scholar]
- Tossavainen T, Rensaa RJ, Johansson M. Swedish first-year engineering students’ views of mathematics, self-efficacy and motivation and their effect on task performance. Int J Math Educ Sci Technol 2021; 52(1):23-38. doi: 10.1080/0020739x.2019.1656827 [Crossref] [ Google Scholar]
- Zakariya YF. Improving students’ mathematics self-efficacy: a systematic review of intervention studies. Front Psychol 2022; 13:986622. doi: 10.3389/fpsyg.2022.986622 [Crossref] [ Google Scholar]
- Sakellariou C. The reciprocal relationship between mathematics self-efficacy and mathematics performance in US high school students: instrumental variables estimates and gender differences. Front Psychol 2022; 13:941253. doi: 10.3389/fpsyg.2022.941253 [Crossref] [ Google Scholar]
- Doménech-Betoret F, Abellán-Roselló L, Gómez-Artiga A. Self-efficacy, satisfaction, and academic achievement: the mediator role of students’ expectancy-value beliefs. Front Psychol 2017; 8:1193. doi: 10.3389/fpsyg.2017.01193 [Crossref] [ Google Scholar]
- Street KES, Malmberg L-E, Schukajlow S. Students’ mathematics self-efficacy: a scoping review. ZDM – Mathematics Education 2024; 56(2):265-80. doi: 10.1007/s11858-024-01548-0 [Crossref] [ Google Scholar]
- Özcan B, Kültür YZ. The Relationship Between Sources of Mathematics Self-Efficacy and Mathematics Test and Course Achievement in High School Seniors. Sage Open 2021; 11(3):21582440211040124. doi: 10.1177/21582440211040124 [Crossref] [ Google Scholar]
- Zimmerman BJ. Self-efficacy: an essential motive to learn. Contemp Educ Psychol 2000; 25(1):82-91. doi: 10.1006/ceps.1999.1016 [Crossref] [ Google Scholar]
- Usher EL, Pajares F. Sources of self-efficacy in mathematics: a validation study. Contemp Educ Psychol 2009; 34(1):89-101. doi: 10.1016/j.cedpsych.2008.09.002 [Crossref] [ Google Scholar]
- May DK. Mathematics Self-Efficacy and Anxiety Questionnaire [dissertation]. University of Georgia; 2009.
- Vallerand RJ, Pelletier LG, Blais MR, Briere NM, Senecal C, Vallieres EF. The academic motivation scale: a measure of intrinsic, extrinsic, and amotivation in education. Educ Psychol Meas 1992; 52(4):1003-17. doi: 10.1177/0013164492052004025 [Crossref] [ Google Scholar]
- Sukoco H, Suharjo I. Mathematics self-efficacy scale based on computer. Indones J Math Educ 2019; 2(1):43-53. doi: 10.31002/ijome.v2i1.1248 [Crossref] [ Google Scholar]
- Cook DA, Artino AR Jr. Motivation to learn: an overview of contemporary theories. Med Educ 2016; 50(10):997-1014. doi: 10.1111/medu.13074 [Crossref] [ Google Scholar]
- MacAfee E, Comeau G. The impact of the four sources of efficacy on adolescent musicians within a self-modeling intervention. Contributions to Music Education 2020; 45:205-36. [ Google Scholar]
- Hernández de la Hera JM, Morales-Rodríguez FM, Rodríguez-Gobiet JP, Martínez-Ramón JP. Attitudes toward mathematics/statistics, anxiety, self-efficacy and academic performance: an artificial neural network. Front Psychol 2023; 14:1214892. doi: 10.3389/fpsyg.2023.1214892 [Crossref] [ Google Scholar]
- Alzahrani A, Beh EJ, Stojanovski E. Exploring the association between self-efficacy and future utility beliefs in mathematics: a practical tutorial on correspondence analysis. PLoS One 2023; 18(3):e0282696. doi: 10.1371/journal.pone.0282696 [Crossref] [ Google Scholar]
- Yu W, Zhou S, Zhou Y. Intervention on mathematics self-efficacy: solution-focused brief therapy. Psychol Res Behav Manag 2024; 17:129-45. doi: 10.2147/prbm.s432569 [Crossref] [ Google Scholar]
- Wang C, Li X, Wang HJ. The mediating effect of math self-efficacy on the relationship between parenting style and math anxiety. Front Psychol 2023; 14:1197170. doi: 10.3389/fpsyg.2023.1197170 [Crossref] [ Google Scholar]
- Hiller SE, Kitsantas A, Cheema JE, Poulou M. Mathematics anxiety and self-efficacy as predictors of mathematics literacy. Int J Math Educ Sci Technol 2022; 53(8):2133-51. doi: 10.1080/0020739x.2020.1868589 [Crossref] [ Google Scholar]
- Wong SL, Wong SL. Relationship between interest and mathematics performance in a technology-enhanced learning context in Malaysia. Res Pract Technol Enhanc Learn 2019; 14(1):21. doi: 10.1186/s41039-019-0114-3 [Crossref] [ Google Scholar]
- Yaribeygi H, Panahi Y, Sahraei H, Johnston TP, Sahebkar A. The impact of stress on body function: a review. EXCLI J 2017; 16:1057-72. doi: 10.17179/excli2017-480 [Crossref] [ Google Scholar]
- Lande NM, Ask TF, Sætren SS, Lugo RG, Sütterlin S. The role of emotion regulation for general self-efficacy in adolescents assessed through both neurophysiological and self-reported measures. Psychol Res Behav Manag 2023; 16:3373-83. doi: 10.2147/prbm.s406702 [Crossref] [ Google Scholar]
- Li N, Yang Y, Zhao X, Li Y. The relationship between achievement motivation and college students’ general self-efficacy: A moderated mediation model. Front Psychol 2022; 13:1031912. doi: 10.3389/fpsyg.2022.1031912 [Crossref] [ Google Scholar]
- Shengyao Y, Salarzadeh Jenatabadi H, Mengshi Y, Minqin C, Xuefen L, Mustafa Z. Academic resilience, self-efficacy, and motivation: the role of parenting style. Sci Rep 2024; 14(1):5571. doi: 10.1038/s41598-024-55530-7 [Crossref] [ Google Scholar]
- Steinmayr R, Weidinger AF, Schwinger M, Spinath B. The importance of students’ motivation for their academic achievement - replicating and extending previous findings. Front Psychol 2019; 10:1730. doi: 10.3389/fpsyg.2019.01730 [Crossref] [ Google Scholar]
- Urhahne D, Wijnia L. Theories of motivation in education: an integrative framework. Educ Psychol Rev 2023; 35(2):45. doi: 10.1007/s10648-023-09767-9 [Crossref] [ Google Scholar]